The greatest common divisor between two numbers is defined as the largest value that can divide both numbers.
To compute the greatest common divisor there are many algorithms. One of the fastest is over 2 millennium old. It's called Euclid's algorithm. Here you will be able to learn more about this algorithm and how to program it. Also you will learn how to visualize the number of iterations it needs to find the result.
The algorithm could consist of the following points:
- Let a and b be the two numbers for which we are trying to find the GCD
- Initialize d at 1 and solution also at 1. (Notice 1 divides any number)
- If d divides a and also d divides b, then store d in solution.
- Increase d in one unit
- If d is smaller than a and b repeat step 3.
- The result will be stored in solution.
var a = input()
var b = input()
var d = 1, solution = 1
while (d <= a && d<=b) {
if ((a % d) == 0 && (b % d) == 0) {
solution = d
}
d++
}
output(solution)
Let us take a moment to discuss some of the instructions used in this small code.
First of all to read and write in eSeeCode you need to go to the I/O tag next to the Debug. To read some values we will use the instruction input() and, to write, we use the instruction output().
Also, as in many languages, d++ means increase the value in d by one unit.
Finally to check if d divides a we use the operator %. This will return the reminder of the division between a and d. As an example a%2==0 would mean a is an even number.
Euclid's algorithm is based on a simple fact. Let (a,b) stand for the greatest common divisor between a and b. Then (a, b) = (a, b-a). You can try to prove this statement by considering the set of divisors of each side and showing they are the same set. Generalizing this result we can state the fact that (a,b)=(b,a%b).
Becuase this is a recursive definition we need to define a basic case. In this case it will be when b is 0 (the greatest common divisor will be a). This property gives us an outline for a recursive algorithm. A recursive function is a function that calls itself, and to avoid an infinite loop we need a base case. This is similar to a proof by induction.
function GCD(a, b) {
if (b == 0) {
return a
}
return GCD(b, a % b)
}
var a = input()
var b = input()
output(GCD(a, b))
function square(color, size) {
setColor(color)
beginShape()
repeat (4) {
forward(size)
turnRight(90)
}
endShape()
setColor('black')
repeat (4) {
forward(size)
turnRight(90)
}
}
function gcd(a, b) {
if (a === 0 || b === 0) {
output(a + b)
return a + b
}
steps++
output('(' + a + ', ' + b + ')')
if (a < b) {
var r = b % a
var n = (b - r) / a
var color = getRandomColor()
repeat (n) {
square(color, a * q)
turnRight(90)
forward(a * q)
turnLeft(90)
}
return gcd(a, r)
} else {
var r = a % b
var n = (a - r) / b
var color = getRandomColor()
repeat (n) {
square(color, b * q)
forward(b * q)
}
return gcd(r, b)
}
}
var steps = 0
var a = input()
var b = input()
var q = 300 / Math.max(a, b)
// If you want to use larger numbers substitude the 30 by the longest reasonable measure
goTo(-150, 150)
setSize(4)
forward(a * q)
forward(-a * q)
turnRight(90)
forward(b * q)
forward(-b * q)
turnLeft(90)
writeAt(a, -150 + a * q / 2, 160)
writeAt(b, -160, 150 - (b * q / 2), 90)
setSize(2)
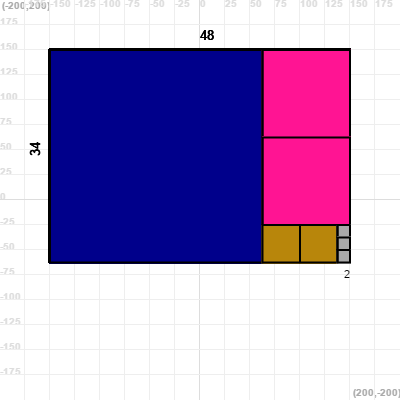
var result = gcd(a, b)
setColor('black')
if (b < a) {
writeAt(result, 150 - (result * q / 2), 150 - (b * q) - 15)
} else {
writeAt(result, -150 + a * q - (result * q / 2), 150 - (b * q) - 15)
}
output('steps: ' + steps)
We are interested in studying the number of calls that our recursive function does. To do so we could build a table for each pair of numbers in a certain range. This would give us an idea on how it changes, but because the variation is slow, it would be tedious and we would need plenty of values to see the behavior. Instead we will represent the number of iterations in a plane.
For a given point (x,y) we will compute how many calls we need to compute the greatest common divisor of x and y. Then we will paint that point with a specific color depending on the number of steps. To simplify the program we will consider the number steps of x and y the same as for y and x, although they differ by one unit. In our case we will use a grid of 400x400 points. The result can be seen in this figure.

function gcd(a, b) {
steps++
if (b == 0) {
return a
}
return gcd(b, a % b)
}
changeAxis(0, 400, 1, -1)
var colors = ['#000000', '#FFFFFF', '#FF00FF', '#EE82EE', '#DA70D6', '#BA55D3', '#9370DB', '#8A2BE2', '#9400D3', '#9932CC', '#8B008B', '#800080', '#4B0082']
var steps = 0
for (var i = 0; i < 400; ++i) {
for (var j = i; j < 400; ++j) {
steps = 0
gcd(j, i)
setColor(colors[Math.trunc(steps - 1)])
goTo(i, j)
arc(0.1)
goTo(j, i)
arc(0.1)
}
}
setColor("black")
setSize(8)
for (var i = 1; i <= 8; ++i) {
writeAt(i * 50, 5, i * 50 - 10)
writeAt(i * 50, i * 50 - 10, 5, 90)
}
We might want to highlight the important lines from this graph.
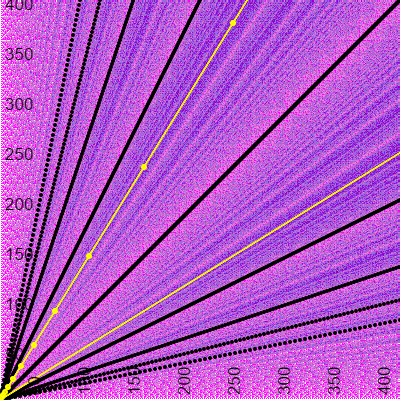
In black we have painted the lines y=kx and the lines y=(1/k)x, where k is a positive integer. We can see that those lines correspond to the same color in figure 1. This is because it only needs one iteration to find the answer.
In yellow we have marked the Fibonacci Numbers and the line y=Phi*x, where Phi refers to the golden ratio. We can see in Figure 1 that this corresponds with the most number of calls. Try to figure out why do you think that this is the case.
As in the previous case, we might want to increase the time allowed to execute the program.
setColor("Black")
for (var k = 1; k < 6; k++) {
for (var i = 0; i < 400; ++i) {
goTo(i, k * i)
arc(1)
goTo(k * i, i)
arc(1)
}
}
setColor("yellow")
var x, y, z
x = 1
y = 1
z = 2
while (z < 400) {
z = x + y
x = y
y = z
goTo(x, y)
arc(2)
}
setColor("yellow")
var k = 1.618034
for (var i = 0; i < 400; ++i) {
goTo(i, k * i)
arc(0.1)
goTo(k * i, i)
arc(0.1)
}
What other ideas would you investigate in this topic? As always any suggestions are welcome. Send us an e-mail at info@eseecode.com or twit us at @eseecode or leave a comment below.